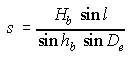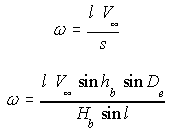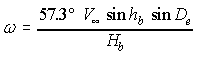After observing several impressive major shower maxima you may have caught the meteor-watching “bug” and ask whether there is anything interesting to see in between the activity periods of major showers. The answer is a clear ‘YES’ since there are the so-called minor showers that have not been investigated nearly as well as the major ones. In addition there are always sporadic meteors to observe, too. There is a great need for reliable observations throughout the whole year and if you have some experience you can contribute a lot to the understanding of all types of meteor activity.
Obtaining the necessary experience is impossible when sitting inside and talking about meteors. Read this chapter carefully and then go outside to observe regularly even if it is cold and uncomfortable! In this way you will soon belong to the handful of people observing throughout the whole year and thus gain the experience to properly observe minor showers.
Choosing the observing field
Most meteors are witnessed centrally in the field of vision. Thus it is important to choose the field center such that meteors appearing there can be easily distinguished from sporadics and associated to the shower(s) under study. In the vicinity of the radiant, shower meteors are slow moving and have short paths while at larger distances from the radiant they resemble sporadics. A field near the radiant seems therefore more favourable. As we have seen in Section 6.1, the main criterion, the direction of the path, also applies more accurately for meteors in the vicinity of the radiant.
From the above one could perhaps conclude that it is best to look directly at the radiant. But we must consider another point too. Which property distinguishes meteors from stars? Their motion. We witness faint meteors in between the hundreds of stars in our field due to their movement. If a faint star appeared for about one second we would not realize it. But that is exactly the scenario which happens when a meteor occurs in the immediate vicinity of the radiant! We need some degree of movement when witnessing a meteor. On the other hand, very fast-moving meteors are easily missed too. Medium velocity is optimal for perception.
Taking into account all the factors discussed above a distance from the centre of the field of view to the radiant(s) under study of 20° to 40° is optimal. Distances of more than 50° should be avoided.
Besides an elevation of 50° to 70° from the horizon and a radiant distance of 20° to 40° , there is an additional point to be taken into account. If you are going to observe several showers at the same time, which is quite possible, you have to take care that their radiants do not lie in one line as seen from your field centre. Otherwise meteors from these radiants cannot be distinguished by their path directions, and distinguishing them by their angular velocity and path length alone will become difficult and more uncertain. Observing, for instance, the Orionids with their radiant near Betelgeuze (beta Ori) and the epsilon-Geminids with their radiant near Pollux (beta Gem) the field centre should be in Taurus/Auriga/Perseus or Canis Minor/Monoceros/Canis Major rather than in Cancer/Ursa Major or Lepus/Eridanus.
When you have chosen the best-situated field you should follow its diurnal motion as long as conditions (elevation of the field about 50° -70° , artificial lights, obstructions, etc.) permit. If you are forced to change the field, note the time of this change and the new field. For analysis the time of such a change should be identical with the boundary of an observing interval.
Criteria for shower association
Generally, particles in a meteoroid stream move in similar orbits, and thus enter the atmosphere parallel to each other at about the same velocity producing a meteor shower. This results in certain characteristics useful for distinguishing them from other meteors not belonging to this shower.
Angular velocity
Meteors of a given shower start to emit light at similar heights above the Earth’s surface. Their velocities are also alike, with only small differences. The deceleration on the luminous path through the atmosphere can be neglected for ordinary meteors; their velocity is reduced by a few percent only. For our purposes we can assume that shower meteors move parallel to each other with a constant velocity.
Thus the apparent angular velocity omega of a shower meteor (in degrees per second) can be calculated by the framed formula below depending on the pre-atmospheric velocity V_infty (km/s), the elevation h_b (degrees) and altitude H_b (km) of its start point, and the angular distance between its end point and the radiant D_e (degrees).
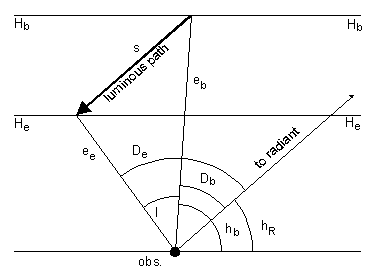
With l being the apparent path length of the meteor and s its true trail length.
For apparent path lengths l shorter than ~30° we find:
Finally, we can write:
The angular velocity omega of a shower meteor is thus well defined for any point in the sky. It is a strict criterion used for shower association.
In the below table the angular velocities omega for different entry velocities V have been calculated. Since the beginning altitude H_b depends mainly on V, characteristic beginning altitudes for individual geocentric velocities were assumed in the calculations.
Table 1 is used to determine the expected angular velocity of shower meteors. For interpolation of values not directly included in the table, please refer to the examples given below the table.
Table 1. Expected angular velocity of shower meteors
V=20 km/s H_b=100 km | V=25 km/s H_b=100 km
h_b= 10° 20° 40° 60° 90° | 10° 20° 40° 60° 90°
|
D= 5° 0.2 0.3 0.6 0.9 1.0 | 0.2 0.4 0.8 1.1 1.3
10° 0.3 0.7 1.3 1.7 2.0 | 0.4 0.9 1.6 2.2 2.5
20° 0.7 1.3 2.5 3.4 3.9 | 0.9 1.7 3.2 4.3 4.9
40° 1.3 2.5 4.7 6.3 7.3 | 1.6 3.2 5.9 8.0 9.3
60° 1.7 3.4 6.3 8.5 9.8 | 2.2 4.3 8.0 11 13
90° 2.0 3.9 7.3 9.8 11 | 2.5 4.9 9.3 13 14
V=30 km/s H_b=100 km | V=35 km/s H_b=100 km
h_b= 10° 20° 40° 60° 90° | 10° 20° 40° 60° 90°
|
D= 5° 0.3 0.5 1.0 1.4 1.6 | 0.3 0.6 1.1 1.5 1.7
10° 0.5 1.1 2.0 2.7 3.1 | 0.6 1.2 2.2 3.0 3.4
20° 1.1 2.1 4.0 5.3 6.2 | 1.2 2.3 4.3 5.8 6.7
40° 2.0 4.0 7.4 10 12 | 2.2 4.3 8.2 11 13
60° 2.7 5.3 10 14 16 | 3.0 5.8 11 15 17
90° 3.1 6.2 12 16 18 | 3.4 6.7 13 17 20
V=40 km/s H_b=100 km | V=50 km/s H_b=110 km
h_b= 10° 20° 40° 60° 90° | 10° 20° 40° 60° 90°
|
D= 5° 0.3 0.7 1.3 1.7 2.0 | 0.4 0.8 1.5 2.0 2.3
10° 0.7 1.4 2.6 3.5 4.0 | 0.8 1.6 2.9 3.9 4.6
20° 1.4 2.7 5.0 6.8 7.9 | 1.6 3.1 5.8 7.8 9.0
40° 2.6 5.0 9.5 13 15 | 2.9 5.8 11 15 17
60° 3.5 6.8 13 17 20 | 3.9 7.8 15 20 23
90° 4.0 7.9 15 20 23 | 4.6 9.0 17 23 26
V=60 km/s H_b=115 km | V=66 km/s H_b=115 km
h_b= 10° 20° 40° 60° 90° | 10° 20° 40° 60° 90°
|
D= 5° 0.5 0.9 1.7 2.3 2.6 | 0.5 1.0 1.9 2.5 2.9
10° 0.9 1.8 3.4 4.5 5.2 | 1.0 2.0 3.7 5.0 5.8
20° 1.8 3.5 6.7 9.0 10 | 2.0 3.9 7.3 10 11
40° 3.7 6.7 13 17 20 | 3.7 7.3 14 18 21
60° 4.6 9.0 17 23 26 | 5.0 10 18 25 29
90° 5.3 10 20 26 30 | 5.8 11 21 29 33
V=70 km/s H_b=126 km
h_b= 10° 20° 40° 60° 90°
D= 5° 0.5 0.9 1.8 2.4 2.8
10° 1.0 1.9 3.6 4.8 5.5
20° 1.9 3.7 7.0 9.4 11
40° 3.6 7.0 13 18 21
60° 4.8 9.4 18 24 28
90° 5.5 11 21 28 32
Examples:
1. Virginid V=35 km/s h_b=60° D_e=40° omega=11°/s
2. Orionid V=66 km/s h_b=30° D_e=60° omega~14°/s
3. Ursid V=33 km/s h_b=50° D_e=30° omega~ 7°/s
Apparent path length
Assuming constant beginning and end altitudes (H_b, H_e) for meteors belonging to a certain shower one can calculate the expected apparent path length l for members of the shower depending on the elevation of the radiant h_R, the elevation of the start point h_b, and the angular distance between the radiant and the start point D_b: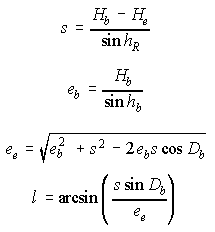
For given beginning and end altitudes, l depends on three quantities: h_R, h_b, and D_b. To visualize this dependence we would have to construct a 4-dimensional diagram which is impossible. This means that the criterion is quite difficult to handle. But calculating l for several combinations of beginning/ending altitudes one finds:
D_b / l ~ constant for D_b < 30°.
This means that the criterion l can be used favourably in the vicinity of the radiant. In that region shower meteors distinguish themselves from sporadics by their short paths. Bearing in mind that the end altitude depends on the particle mass and material it is opportune to assume it is such that the calculated l is considered to be the upper limit for shower membership. Thus it was assumed H_b = 100 km and H_e = 80 km. The result is shown in Figure 2.
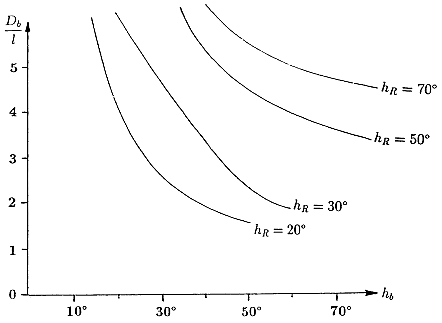 Figure 2 – The quotient D_b / l for D_b < 30° as a function of h_b for several elevations of the radiant h_R. Calculation was carried out using H_b = 100 km, and H_e = 80 km.
Figure 2 – The quotient D_b / l for D_b < 30° as a function of h_b for several elevations of the radiant h_R. Calculation was carried out using H_b = 100 km, and H_e = 80 km.It can be seen that radiants having low elevations produce long meteor paths (small value of D_b / l). The higher the meteor appears in the sky the closer it is to the observer, and thus, the true trail length is seen over a larger angle (apparent path length l). The application of the quantities shown in Figure 2 for shower association is problematic since end altitudes can vary greatly and the path length is much more affected by plotting errors than the direction. Therefore, we can establish only a general rule:
For radiant elevations higher than 30° the apparent path length l of a shower meteor amounts at most to half the distance from the radiant to the start point.
Consequently, the distance between radiant and start point of a plotted meteor on the chart has to be at least twice as long as the meteor path itself if the meteor is a suspected shower member. This rule is not valid for fireballs which generally penetrate deeper into the atmosphere and thus produce longer paths.
Looking at Figure 2, the formulation of the rule seems to be too weak, since factors of 3-5 will be valid for most meteors, but in strengthening the rule there is the danger of classifying a considerable number of shower meteors in the vicinity of the radiant as sporadics, due to short paths being plotted as too long. Experience shows that a factor of two is strong enough for distinguishing sporadic meteors meeting the criteria of path direction and angular velocity, within certain error limits, from real shower meteors.
Path and radiant
As you know from major-shower observations, shower meteors seem to radiate from a certain point in the sky, the radiant. To gain some insight into this, please turn to Figures 3 and 4 which show how observers A, B, C, D and E project a meteor M onto the sky hemisphere as sections of arcs. These great circles concern the meteors belonging to the same radiant and have two poles or intersection points in common: the radiant R above the horizon and the anti-radiant AR below. The plane perpendicular to the great circles through O marks the points at 90° distance from the radiant.
When the chart’s center P is situated at less than 90° from the radiant, the latter may be marked on the same plane as that of the map by use of the usual projection formulae. The backward extensions of the shower meteors meet the radiant. For your convenience the Shower Calendar includes a table giving the positions and drifts of the radiants.
When the radiant is at more than 90° from the map’s center, it cannot be projected onto this chart, but the anti-radiant may be. Its position results from:
delta_AR = – delta_R
alpha_AR = alpha_R ± 180°
Now the forward prolongation of the meteor trail meets the anti-radiant. This also become obvious from Fig. 4.
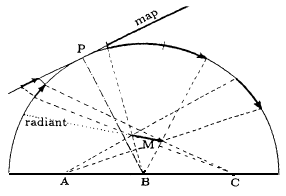 Figure 3 – Side view of the trajectory being projected on the celestial sphere and on the map. P denotes the map center (= projection center), and M is the meteor trajectory.
Figure 3 – Side view of the trajectory being projected on the celestial sphere and on the map. P denotes the map center (= projection center), and M is the meteor trajectory.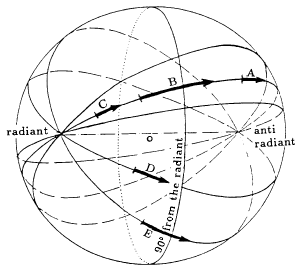 Figure 4 – View of the sphere on which the meteor’s trajectory was projected from different places. A, B, and C are situated on the same meridian (great circle). Other observers (D, E) may see it on other great circles.
Figure 4 – View of the sphere on which the meteor’s trajectory was projected from different places. A, B, and C are situated on the same meridian (great circle). Other observers (D, E) may see it on other great circles.Due to perturbations and different ejection conditions from their parent object, the individual particles of a meteor shower do not move on exactly the same orbit. Thus they do not all enter the atmosphere exactly parallel to one another. The result of this is that a radiant is not a point but an area of a certain size whose dimensions depend on how widely the individual orbits are spread, and on the geometrical conditions of how the stream encounters the Earth, and thus differs from shower to shower (Kresák & Porubcan, 1970).
If you plot shower meteors, their backward extensions will form a radiant area considerably larger than the radius obtained from photographic observations. This is due to plotting errors. These errors will be reduced for experienced observers but generally they cannot be avoided. When trying to decide whether a meteor belongs to a certain shower or not the question arises as to how large a radiant area can safely be assumed. Making it too large means the sporadic pollution becomes too strong, i.e. several sporadic meteors will meet the radiant accidentally. If the radiant area is too small a certain number of shower meteors will be classified as sporadics because of the plotting errors. The optimum radiant diameters for shower association are given in Tables 3 and 4.
Observing a meteor
When a meteor appears keep a cool head. Try to store the phenomenon as a whole in your memory. Then keep looking at the sky in order to memorize the following data (in this order):
- The most important information is its direction rather than the exact start/end points. Memorize it corresponding to the background stars, e.g. in between which stars the meteor passed or to which ones it can be traced back or prolonged.
- Maximum magnitude:
Estimate this by comparing it to the brightness of the nearby stars you memorized at the beginning of the watch. - Angular velocity:
In order to have a quantity that can be compared to an expected value for shower association you should estimate this in degrees per second. This is not difficult. In your imagination you make the meteor move for one second. The time span of one second can be easily reproduced and the sensation of the angular velocity you have still in your memory. The path length in degrees the meteor would have reached after moving for one second is its angular velocity in degrees per second. Once you have some experience you will have the scale fixed in your memory and can then estimate the angular velocity directly without this procedure. Do not try to estimate the duration and to obtain the angular velocity by dividing the path length by the duration. The duration is very difficult and uncertain to estimate and the path length is affected by plotting errors, thus the resulting uncertainty in the angular velocity is much greater than if you convert the sensation of the velocity directly into degrees per second. The graphs below gives you an idea about the accuracy experienced observers achieve.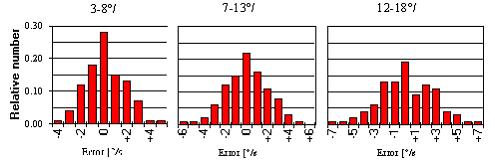
- Persistent train:
Give its duration in seconds. Very short trains, the so-called wakes, may be simply marked with a “+”. Long-duration trains of bright meteors can show interesting behaviors of decay. They might become bended or distorted, and you should note details on these phenomena. - Color:
Note that it is generally impossible to detect colors for meteors fainter than magnitude +2. This information is of least value of all the data.
Now you can switch on your dim red torch and choose the chart the meteor is best plotted on, i.e. that chart for which the meteor occurs nearest the center. It is worthwhile preparing your stock of charts such that you know the sequence exactly and you may find the most suitable chart without interruption of the observation, needing to look at the paper only then. The next step is the identification of the stars you used for memorizing the path on the chart. Since the charts contain all stars down to magnitude +6.5mag you should readily find them on the chart unless your limiting magnitude is considerably better than +6.5mag. This step is one source of plotting errors, therefore be careful! If you are sure that you have found the right stars you can plot the meteor from memory. For identification the plot must be numbered. Finally, you should estimate the accuracy of the plot with the following scale:
- very accuratey
- medium accuracy
- poor accuracy
For your first observations, plotting will require some time. Do not hurry: take the time to plot carefully. Quality is most important! The time needed for plotting will reduce rapidly with your increasing experience. Experienced observers need on average 10 to 30s.
After plotting, look at your watch to record the time. Unless you saw a fireball the time needs to be a rough estimation only. An accuracy of 1 minute is sufficient. Then the remaining data should be recorded. You can complete a list as shown below.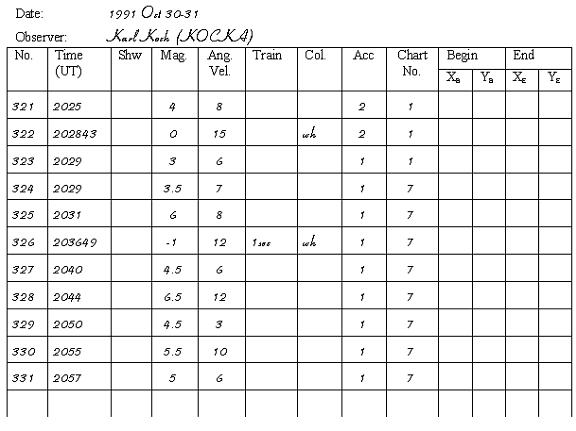
In order to save some observing time you can record the data on tape. In this case you should fill in the list after the observation. For plotting meteors you will need a certain amount of time, during which you look at your chart rather than at the sky. Therefore, the effective observing time must be reduced by the plotting time. It would be a major effort to record the time you used for plotting every individual meteor, so it is better to determine an average time for plotting one meteor as outlined below.
Use a stopwatch that is able to add times. When you start looking at the chart start the stopwatch, when you resume looking at the sky stop it. (For example, start the stopwatch for plotting, stop after the plot is done at, say 38.4 s (0:38.4), when the next meteor occurs after some minutes start again at 38.4 s, stop after the plot at 1:22.6, and so on). After observing a number of meteors, say 25, the stopwatch displays the time you did not observe the sky, say 16 min 40 s. Dividing this time by 25 meteors you obtain an average plotting time of 40 s per meteor (16 min 40 s = 1000 s, 1000 s / 25 meteors = 40 s / meteor). If you observed, for example 29 meteors in an interval, the total plotting time to be subtracted from the effective time is 29 meteors times 40 s/meteor = 1160 s = 19 m 20 s ~ 19 min. On the report form (interval analysis) these quantities have to be filled in on the line: “Time for plotting _______ s / meteor, _______ min total”. For experienced observers the average time for plotting a meteor is a constant that should be checked about twice a year by the procedure described above. Beginners should check it regularly, say every third meteor watch.
Shower analysis
In the Section “Criteria for shower association”, you have learned about the criteria a meteor has to meet before it can be considered as a highly probable shower member. Now the practical use of the criteria will be examined. On a free afternoon you should allow enough time to analyse your observation.
First of all, take the most recent version of IMO’s working list of meteor showers from the Shower Calendar and select all the showers active on the date of your observation. Then plot their radiant positions valid for that date onto the charts. Take into account the radiant drift by using the drift tables!
Table 2. Error limits for the angular velocity omega to be assumed for shower association.
angular velocity [° /s] 5 10 15 20 30 permitted error [° /s] 3 5 6 7 8
Table 3. Optimum radiant diameters to be assumed for shower association of minor shower meteors to well- and moderately defined radiants as a function of the radiant distance of the meteor.
radiant distance optimum radiant
of the meteor [° ] diameter [° ]
15 14
30 17
50 20
70 23
Table 4. Optimum radiant sizes (in alpha, delta) to be assumed for shower association of complex radiants.
radiant distance of the meteor 15° 30° 50° 70° delta-Cancrids (DCA) 20°/13° 24°/18° 26°/21° 34°/30° Virginids (VIR) 30°/20° 31°/23° 33°/26° 40°/34° Sagittarids (SAG) 30°/20° 31°/23° 33°/26° 40°/34° Southern Taurids (STA) 20°/13° 24°/18° 26°/21 34°/30° Northern Taurids (NTA) 20°/13° 24°/18° 26°/21° 34°/30° Puppids (PUP) 20° 24° 26° 34°
The radiant diameters are plotted as concentric circles (or ellipses for the complex radiants) onto the chart (see Tables 3 and 4 above). The scale is not constant over the chart. Therefore, a radiant of 20° diameter in the center of the chart appears smaller than one of the same diameter near the edge of the chart. Table 5 shows the variation of scale over the chart. As an example, a radiant of 20° diameter at 150 mm distance from the center of the chart appears as a circle of 104 mm diameter.
Table 5. Scale s in mm/° for different distances d to the center of the Gnomonic Atlas Brno charts (valid for the original projection radius R = 160.43 mm).
d [mm] 0 50 100 120 150 170 200 220 s [mm/°] 2.8 3.1 3.9 4.4 5.2 5.9 7.1 8.1
After plotting the radiants onto the charts you have to analyze each meteor separately. Use a ruler of at least 30 cm length to extend the meteor path backwards. If the backward extension meets a radiant area of the corresponding size the meteor may belong to this shower, i.e. the necessary condition that the “path can be extended backwards to the radiant” is fulfilled. It may happen that a meteor belongs to a radiant that is plotted on a neighbouring chart. The backward extension is prolonged onto this other chart by using stars which are present on both charts, i.e. stars in the overlapping region. You have to identify stars crossed or closely passed by the line on the neighboring chart and plot the line in the corresponding position to these stars onto the second chart.
In the next step, we analyze the condition that “the path length must be shorter than half the angular distance of the radiant to the start point”. Since this is a rough measure only, we can neglect the variable scale of the chart. The distances are measured using the ruler and compared. If the condition is fulfilled we can check the next condition.
It reads “the angular velocity has to correspond to the expected value within the error limits given in Table 2. To check this condition you need a planisphere valid for the latitude of your observing site to determine the elevation of the start point of the meteor, and Table 1. Besides the start elevation you also have to determine the angular distance between the radiant and the end point of the meteor.
You may estimate the radiant distance on the planisphere with sufficient accuracy. Alternatively, estimate the distance of the meteor to the radiant comparing with distances between stars as given in the following table.
Table 6. Distances between bright stars as shown on Atlas Brno charts. The distances are rounded to 5-degree steps.
Chart 1 alpha Per -- alpha Aur 20 Chart 5 alpha Boo -- alpha CrB 20
alpha Per -- alpha UMi 40 alpha Boo -- alpha Vir 35
alpha Per -- alpha Cyg 60 alpha Vir -- eta UMa 60
Chart 2 alpha UMa -- eta UMa 25 Chart 6 eps Peg -- alpha Aql 30
alpha UMi -- alpha Aur 45 alpha Aql -- alpha Cyg 40
alpha Gem -- beta Leo 60 alpha And -- alpha Aql 65
alpha UMi -- beta Leo 75
Chart 7 alpha Tau -- Pleiades 15
Chart 3 alpha UMi -- beta UMi 15 alpha And -- beta Cet 50
alpha Cyg -- alpha Lyr 25 alpha And -- alpha Tau 60
alpha Lyr -- alpha CrB 40
alpha Cyg -- eta UMa 65 Chart 8 alpha Leo -- beta Leo 20
alpha Leo -- alpha CMi 35
Chart 4 alpha Gem -- beta Gem 5 beta Crv -- beta Gem 85
alpha Ori -- beta Ori 20
alpha Tau -- alpha CMi 45 Chart 9 alpha CrB -- alpha Her 25
alpha Aur -- alpha Ori 55 alpha Aql -- alpha Her 40
alpha Aql -- alpha Sco 60
Next, determine the elevation of the start point using the planisphere. Now take Table 1 and determine the expected angular velocity according to the entry velocity V, radiant distance D and elevation h_b which we just obtained. This value has to be compared to the one you estimated during the observation. If the difference lies within the error limit, the condition “angular velocity” is fulfilled. The error limits to be used are shown in Table 2. The table has to be read as in this example: “If the angular velocity was expected to be 15° /s, the condition is fulfilled if the estimated value lies in the range 9-21° /s.
If the meteor fulfills all three criteria it can be considered a shower member. Sometimes it may happen that a meteor fulfills the conditions for shower membership of two different showers. In this case you have to choose the most probable shower, i.e. that shower the conditions are best fulfilled for. It is impossible to consider one meteor to be a member of two or more different showers. You must decide in favour of one shower even if the probability of the meteor’s belonging to two showers is similar.
The features of minor-shower observations
Minor showers are called so since they produce little activity for the visual observer. Generally we define a minor shower as being one whose maximum hourly rate (HR) is less than about 10. Admittedly, this is an arbitrary limit but it is a suitable one for our purposes. It does not make sense to define the limit distinguishing between minor/major showers using their ZHR. The observing technique described here is appropriate when the observed number of meteors does not exceed a certain limit, because this method leads to a certain amount of dead-time. Of course, the time loss must not be significant for the aim of the observation. As already pointed out elsewhere, the main goal of visual observations is the reliable determination of physical shower parameters. Therefore, we consider showers which produce less than 10 meteors per hour to be minor showers. For these, plotting is an essential observing method.
This means the number of shower meteors visible during an observation is considerably smaller than for major showers. These small numbers cause specific problems that we now deal with. Strictly speaking, at the beginning and the end of their activity periods, major showers are effectively minor ones as they suffer from the same problems.
Sporadic activity occurs throughout the year. In the sky the paths of sporadic meteors seem to be nearly randomly distributed. Thus sometimes it happens that the backwards extension of a sporadic meteor track accidentally meets with a shower radiant. Thus shower data usually contain a certain contribution from sporadic meteors. This effect is called “sporadic pollution” and is of the order of 1-2 meteors per hour (m/h).
Imagine a sporadic pollution of 2 m/h. Observing a major shower of 80 meteors per hour, the relative error result is only 2.5% but for a minor shower of 4 m/h it amounts to 50%! Therefore, sporadic pollution is the main problem in observing minor showers. If we want to obtain reliable results we must reduce it. In the following sections you will learn how this can be achieved.
You will see that this requires a lot of knowledge and experience. Tens of observing hours will be necessary to obtain sufficient skill. But are your results obtained in this learning phase completely worthless for analyses? By no means! As long as you think that you are still unable to provide reliable data for the minor showers, simply report the total of meteors seen. In the table of the report form “Observed numbers of meteors per period and per shower” only fill in the column “Tot” and in the table “Magnitude distributions” only give the total magnitude distribution. Even these data about the total activity can be used for some analyses.
In this way you can learn step by step, without the pressure to report the whole bulk of necessary data in the correct way from the first observations. In this learning phase, try to plot the meteors, to report all the data, and to assign the meteors to the different showers as outlined in this chapter until you estimate that your data can now be considered reliable.
It may also be that you do not wish to go so deeply into meteor observing. In this case try to plot the meteors you see using the method described in Section 7 and send the recorded meteor data and the maps to the IMO officer for visual observations. This means you are not forced to deal with the rather difficult problems of minor-shower observations, but despite this fact, your data will be of scientific use.